Design Note 355: Op Amp Selection Guide for Optimum Noise Performance
Introduction
Linear Technology continues to add to its portfolio of low noise op amps. This is not because the physics of noise has changed, but because low noise specifications are being combined with new features such as rail-to-rail operation, shutdown, low voltage and low power operation. Op amp noise is dependent on input stage operating current, device type (bipolar or FET) and input circuitry. This selection guide is intended to help you identify basic noise tradeoffs and select the best op amps, new or old, for your application.
Quantifying Resistor Thermal Noise and Op Amp Noise
The key to understanding noise tradeoffs is the fact that resistors have noise. At room temperature, a resistor R has an RMS voltage noise density (or “spot noise”) of VR = 0.13√R noise in nV/√Hz. So a 10k resistor has 13nV/√Hz and a 1M resistor has 130nV/√Hz. Rigorously speaking, the noise density is given by the equation VR = √4kTR, where k is Boltzman’s constant and T is the temperature in degrees Kelvin. This dependency on temperature explains why some low noise circuits resort to super-cooling the resistors. Note that the same resistor can also be considered to have a noise current of IR = √4kT/R or a noise power density PR = 4kT = 16.6 • 10–21W/Hz = 16.6 zeptoWatts/Hz independent of R. Selecting the right amplifier is simply finding which one will add the least amount of noise above the resistor noise.
Don’t be alarmed by the strange unit “/√Hz.” It arises simply because noise power adds with bandwidth (per Hertz), so noise voltage adds with the square root of the bandwidth (per root Hertz). To make use of the specification, simply multiply it by the square root of the application bandwidth to calculate the resultant RMS noise within that bandwidth. Peak-to-peak noise, as encountered on an oscilloscope for example, will be about 6 times the total RMS noise 99% of the time (assuming Gaussian “bell curve” noise). Do not rely on the op amp to limit the bandwidth. For best noise performance, limit the bandwidth with passive or low noise active filters.
Op amp input noise specifications are usually given in terms of nV/√Hz for noise voltage and pA/√Hz or fA/√Hz for noise current and are therefore directly comparable with resistor thermal noise. Due to the fact that noise density varies at low frequencies, most op amps also specify a typical peak-to-peak noise within a “0.1Hz to 10Hz” or “0.01Hz to 1Hz” bandwidth. For the best ultralow frequency performance, you may want to consider a zero drift amplifier like the LTC2050 or LTC2054.
Summing the Noise Sources
Figure 1 shows an idealized op amp and resistors with the noise sources presented externally. The equation for the input referred RMS sum of all the noise sources, VN(TOTAL) is also shown. It is this voltage noise density, multiplied by the noise gain of the circuit (NG = 1 + R1/R2) that appears at the output.
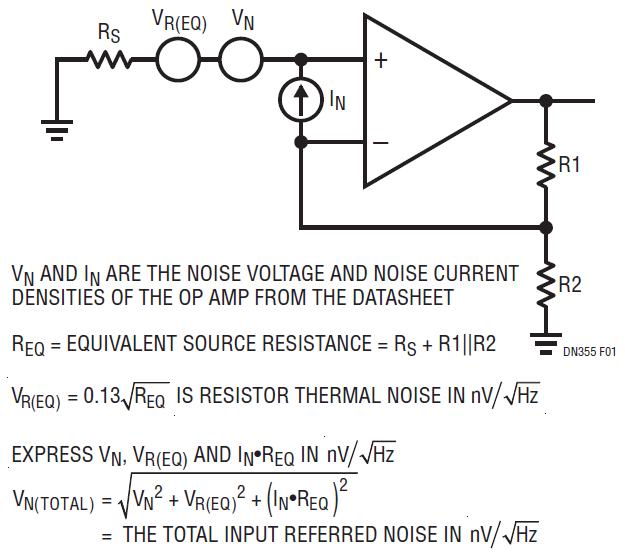
Figure 1. The Op Amp Noise Model. VN and IN Are Op Amp Noise Sources (Correlated Current Noise Is Not Shown). VR(EQ) Is the Voltage Noise Due to the Resistors.
From the equation for VN(TOTAL), we can draw several conclusions. For the lowest noise, the values of the resistors should be as small as possible, but since R1 is a load on the op amp output, it must not be too small. In some applications, such as transimpedance amplifiers, R1 is the only resistor in the circuit and is usually large. For low REQ, the op amp voltage noise dominates (as VN is the remaining term); for very high REQ, the op amp current noise dominates (as IN is the coefficient of the highest order REQ term). At middle values of REQ, the resistor noise dominates and the op amp contributes little significant noise. This is the ROPTIMUM of the amplifier and can be found by taking the quotient of the op amp’s noise specs: VN/IN = ROPT.
Selecting the Best Op Amps
Figure 2 shows plots of voltage noise density of the source resistance and of various op amps at three different frequencies. Each point labeled by an op amp part number is that part’s voltage noise density plotted at its ROPT.
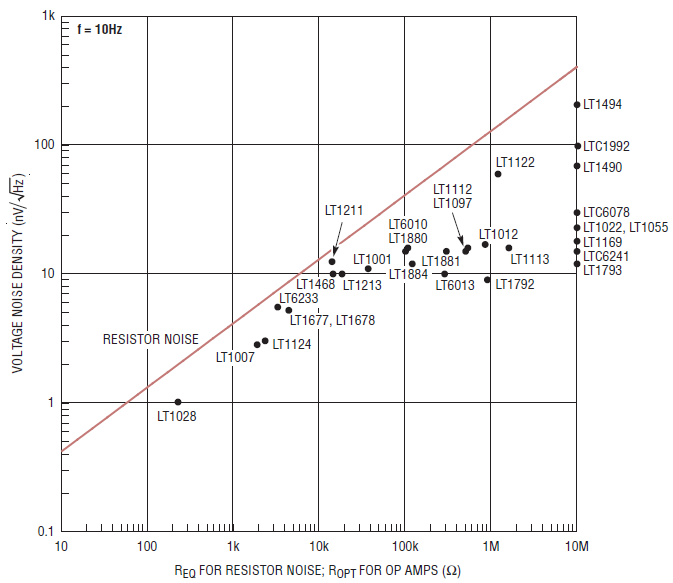
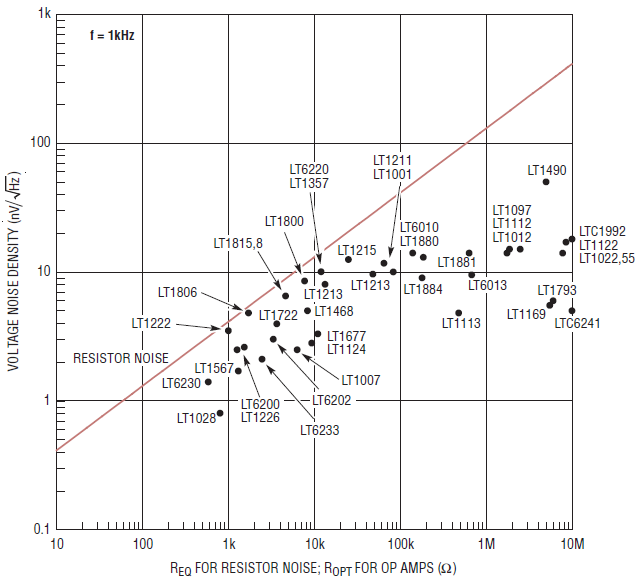
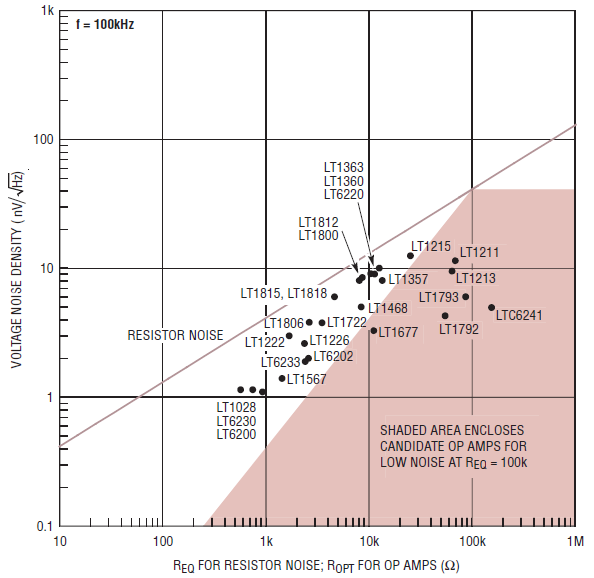
Figure 2. Use These Three Plots to Find the Best Low Noise Op Amps for Your Application
Use the graph with the most applicable frequency of interest. Find your source resistance on the horizontal axis and mark that resistance at the point where it crosses the resistor noise line. This is the “source resistance point.” The best noise performance op amps are under that point, the further down the better.
For all candidate op amps, draw a horizontal line from your source resistance point all the way to the right hand side of the plot. Op amps beneath that line will give good noise performance, again the lower the better. Draw another line from the source resistance point down and to the left at one decade per decade. Op amps below that line are also good candidates.
If you still can’t find any candidates, then you have a very low source impedance and should use op amps that are closest to the bottom. In such cases, paralleling of low noise op amps is also an option.
Conclusion
Noise analysis can be a daunting task at first and is an unfamiliar territory for many design engineers. The greatest influence on overall noise performance is the source impedance associated with the signal. This selection guide helps the designer, whether novice or veteran, to choose the best op amps for any given source impedance.
